Ptychography Method
One of the most fundamental challenges in electron microscopy imaging is phase reconstruction given only the intensity data during measurement processes. This problem occurs because the current detector hardware used in the implementation is unable to record phase information of the exit wave that passes through the specimen under test. Since the phase information is necessary to improve image resolution, to understand the interaction of electrons and atoms within a material, and in particular to recover the electrostatic potential of the specimen, the phase retrieval algorithm is crucial for the application in electron imaging.
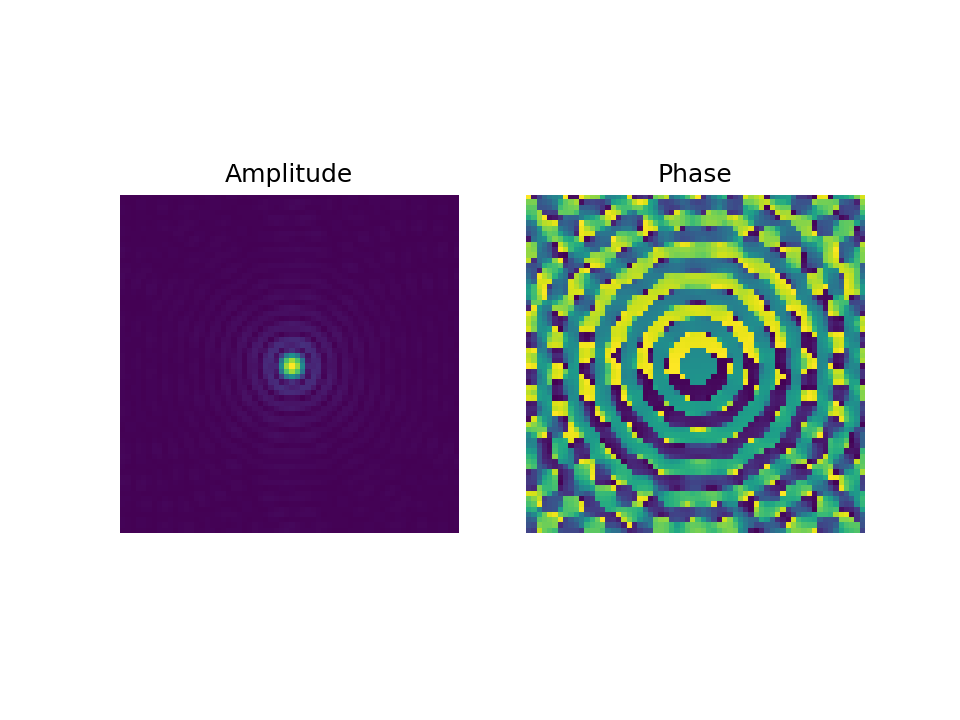
Ptychography is a method to address the phase retrieval problem by processing multiple intensity diffraction patterns stemming from overlapping illuminations of the object. In the literature, the aberration-free illumination given by the electron wave incident is also called the probe, where the structure is modelled by a Bessel function of the first order \(J_1\). The two-dimensional probe \(\mathbf{P} \in \mathbb{C}^{N \times N} \), which depends on the aperture sizes \(q_{\text{max}}\), is given by
$$
\begin{equation*}
\begin{aligned}
\small
p_{y,x} &= \pi q_{\text{max}}^2 \left(\frac{2J_1\left(2 \pi q_{\text{max}} |\mathbf{r}| \right)}{2\pi q_{\text{max}}|\mathbf{r}|} \right),
\end{aligned}
\end{equation*}
$$
where \(\quad y,x \in [N] \) represents discrete grid of the illumination} and \(|\mathbf{r}| = \sqrt{ x^2 + y^2}\).
The intensity of this function, sometimes also called Airy disk, is shown in the following


References:
[1] An improved ptychographical phase retrieval algorithm for diffractive imaging
[2] Experimental tests on double-resolution coherent imaging via STEM
[3] The theory of super-resolution electron microscopy via Wigner-distribution deconvolution
[4] Ptychographic transmission microscopy in three dimensions using a multi-slice approach
[5] Diffraction contrast of electron microscope images of crystal lattice defects - II. The development of a dynamical theory
[6] Advanced computing in electron microscopy