Wigner Distribution Deconvolution
One of the most fundamental questions in ptychography is whether we can estimate both the object transfer function and the probe's illumination given only the intensity of diffraction patterns, also coined as 'blind ptychography'. In general, this problem is difficult because we can have different phase functions without altering the intensity of diffraction patterns. In contrast to the SSB method that has been discussed earlier by assuming a weak phase object, we can directly expand the formula that models the measurement process.
Suppose we have an object transfer function in terms of the coordinate \( \mathbf{r} \in \mathbb{R}^2 \), where the vector \( \mathbf{r} \) represents the two-dimensional coordinate position of our object \( O\left(\mathbf{r}\right) \). Generally, we have two-dimensional grids for all coordinate points. In the scanning transmission electron microscopy (STEM) setting, we raster the probe position according to its scanning coordinate. Hence, we can have an equation that models the acquisition process
$$
I(\mathbf q, \mathbf R) = |\mathcal{F} \left( p\left(\mathbf{r}- \mathbf{R}\right)) O\left(\mathbf{r}\right) \right) |^2,
$$
where in our notation \(\mathbf{q} \in \mathbb{R}^2\) and \(\mathbf{R} \in \mathbb{R}^2\) are the diffraction space or Fourier transform on the coordinate position of the object and the shift coordinate, respectively. It should be noted that the Fourier transform \(\mathcal{F} \) is applied to the coordinate position of our object. By expanding the square function as the product with its complex conjugate, we can write as follows
$$
\begin{equation}
\begin{aligned}
I\left(\mathbf q, \mathbf R\right) &= |\left(p\left(\mathbf{q}\right) e^{-i 2\pi \mathbf{q}\mathbf{R} } \right) \circledast_{\mathbf{q}} O\left(\mathbf{q}\right)|^2
\end{aligned}
\end{equation}
$$
Applying two-dimensional convolution and Fourier transform on the scanning positions \(\mathbf{R} \), we end up with the convolution between the probe's and the object's autocorrelation as follows
$$
\begin{equation}
\begin{aligned}
I\left(\mathbf q, \mathbf Q\right) &= O\left(\mathbf{q}\right) \overline{O\left(\mathbf{q} - \mathbf{Q} \right)} \circledast_{\mathbf{q}} p\left(\mathbf{q}\right) \overline{p\left(\mathbf{q} + \mathbf{Q} \right)}
\end{aligned}
\end{equation}
$$
Now, if we process the intensity of the diffraction pattern again, not in the diffraction space but instead on the coordinate of the object, we can apply two-dimensional inverse Fourier transform on \( \mathbf q\). Consequently, using the relation between convolution and Fourier transform, we have product instead of convolution, where the autocorrelation now becomes the so-called Wigner function or ambiguity function for both object \(\mathcal{W}_O(\mathbf{r},\mathbf{Q})\) and probe \(\mathcal{W}_p(\mathbf{r},\mathbf{Q})\), respectively,
$$
\begin{equation}
\begin{aligned}
I\left(\mathbf r, \mathbf Q\right) &= \mathcal{W}_O(\mathbf{r},\mathbf{Q}) \mathcal{W}_p(\mathbf{r},\mathbf{Q}).
\end{aligned}
\end{equation}
$$
Thereby, we inherently have a deconvolution process from Fourier transform of the convolution operator. Moreover, we can estimate the Wigner function of the object given the division process. In the implementation, one usually should add Wiener filtering to avoid numerical instability when dividing with an element that is close to zero, by adding a small factor \(0 < \epsilon < 1\)
$$
\begin{equation}
\begin{aligned}
\mathcal{W}_O(\mathbf{r},\mathbf{Q}) &= \frac{I\left(\mathbf r, \mathbf Q\right) \overline{\mathcal{W}_p(\mathbf{r},\mathbf{Q})} }{ |\mathcal{W}_p(\mathbf{r},\mathbf{Q})|^2 + \epsilon}.
\end{aligned}
\end{equation}
$$
It should be noted that, since in reality we do not know both \(\mathcal{W}_O(\mathbf{r},\mathbf{Q})\) and \(\mathcal{W}_p(\mathbf{r},\mathbf{Q})\), the algorithm starts by initializing the Wigner function of the probe \(\mathcal{W}_p(\mathbf{r},\mathbf{Q})\) using Airy function with aberration-free condition to estimate the Wigner function of the object \(\mathcal{W}_O(\mathbf{r},\mathbf{Q})\). Since our goal is to estimate the object and not its Wigner function, we can apply Fourier transform on the object coordinate \( \mathbf{r} \) to get \( \hat O\left(\mathbf{q}\right) \overline{\hat O\left(\mathbf{q}- \mathbf{Q} \right)} \). Taking \( \mathbf{q} = 0\) and applying inverse Fourier transform on \( \mathbf{Q}\), we arrive at \(\overline{\hat{O}(\mathbf{R})}\), which is our object at a specific scanning point \( \mathbf{R}\). Overall, the procedure to estimate the object and the probe is called the Wigner Distribution Deconvolution (WDD) [1].
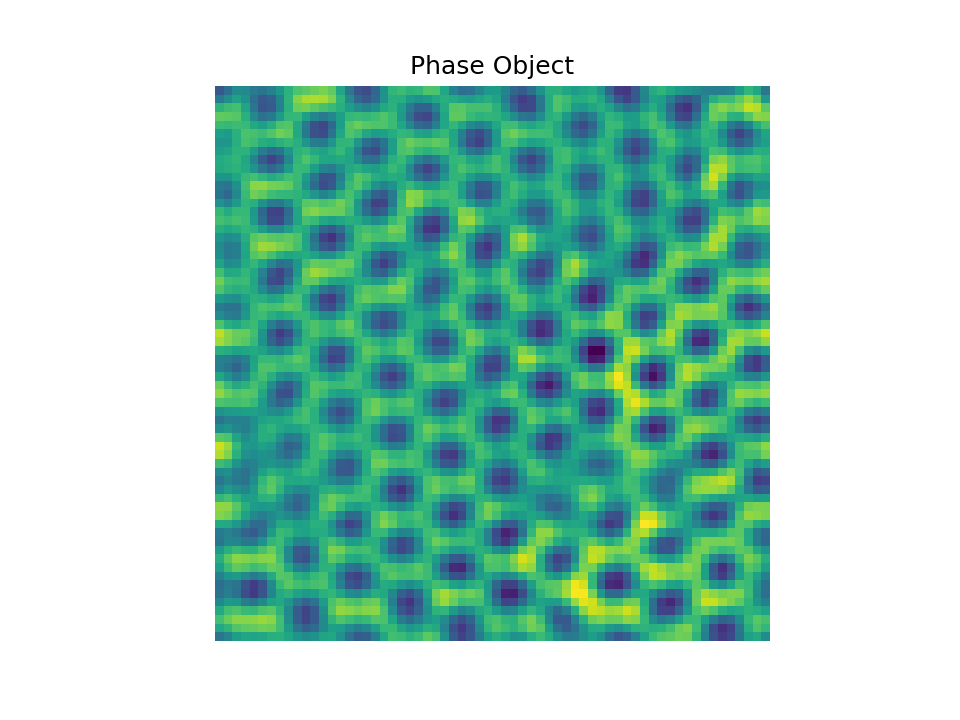
In order to visualize the process, experimental data of the specimen under test is presented. Suppose we have four-dimensional electron microscopy datasets, i.e., two-dimensional scanning points where for each scanning point we have an image representing the intensity of diffraction patterns, as visualized in the following .
. .
.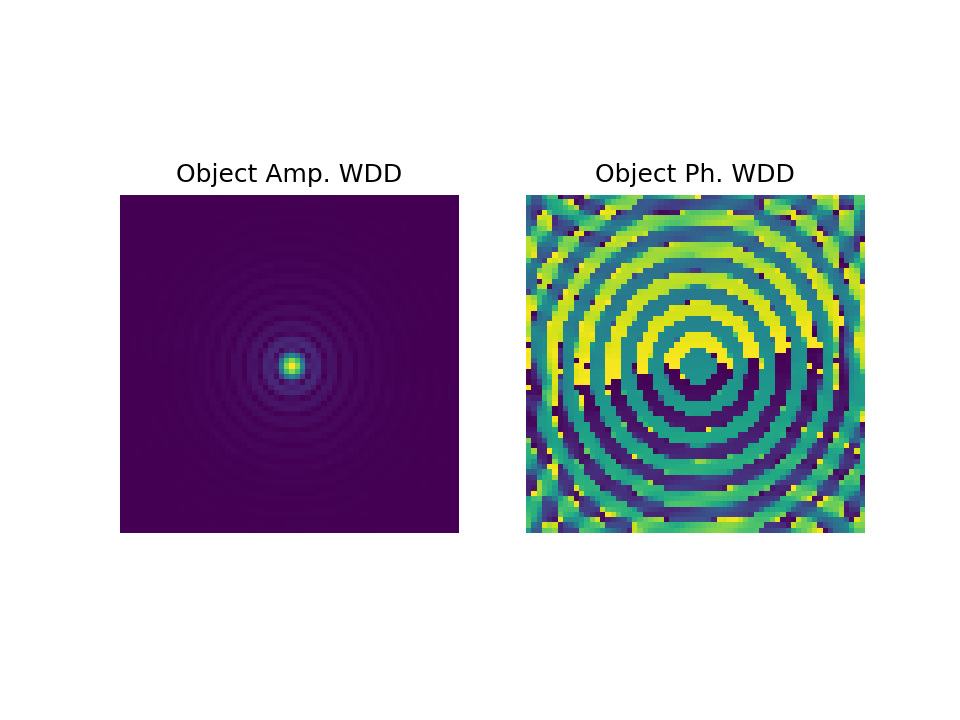
In order to visualize the process, experimental data of the specimen under test is presented. Suppose we have four-dimensional electron microscopy datasets, i.e., two-dimensional scanning points where for each scanning point we have an image representing the intensity of diffraction patterns, as visualized in the following
 .
. .
.
References:
[1] The theory of super-resolution electron microscopy via Wigner-distribution deconvolution\