One fascinating property of the Fourier transform in higher dimensions is the Fourier slice theorem. This theorem states that if we take a slice of Fourier-transformed data through the zero frequency, it is equivalent to the Fourier transform of the projected data. For example, in the case of a two-dimensional Fourier transform, such as with an image, this equality is expressed as a one-dimensional Fourier transform of the projected image itself [1,2].
Suppose we have 2D function \(p(x,y)\), the projection can be written as

\[\begin{equation*} p(x) = \int_{-\infty}^{\infty} p(x,y) dy \end{equation*}\]


Now observe the 2D Fourier transform \(\widehat{p}(k_x,k_y) = \mathcal{F}_{2D} \left( p(x,y)\right)\)

\[\begin{equation*} \widehat{p}(k_x,k_y) ) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} p(x,y) e^{-2\pi(x k_x + y k_y)} dx dy \end{equation*}\]

Focusing on the slice at the center frequency at \(y-\)axis, i.e., \(k_y = 0\), we have

\[\begin{equation*} \begin{aligned} \widehat{p}(k_x,0) &= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} p(x,y) dy \, e^{-2\pi x k_x} dx \\&= \int_{-\infty}^{\infty} p(x) e^{-2\pi x k_x} dx = \mathcal{F}_{1D} \left( p(x)\right) \end{aligned} \end{equation*}\]

This is a 1D Fourier transform on the projection. Additionally, the projection in the discrete setting is the summation on the one axis. The following figure visualizes this property.


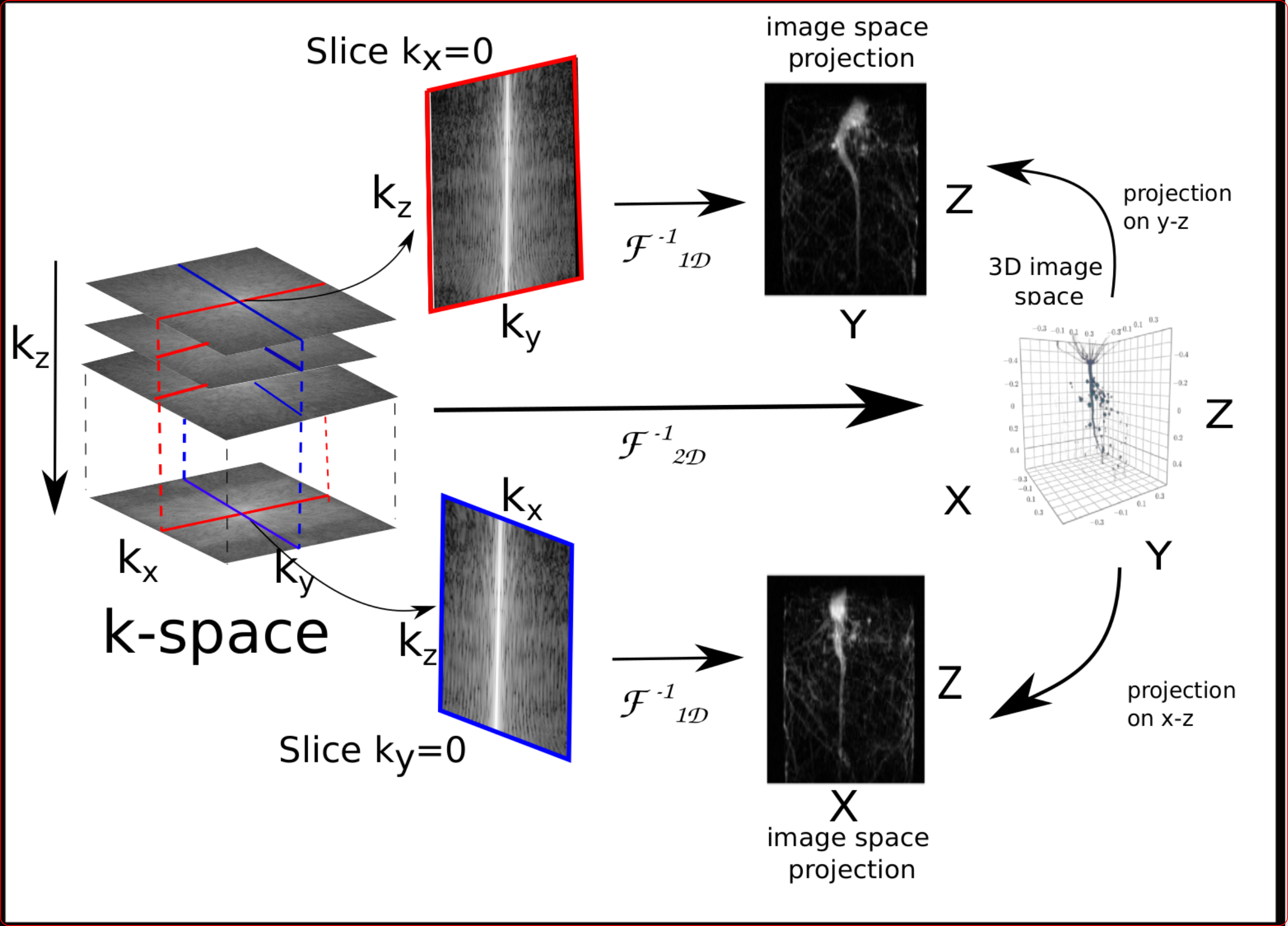
This property is widely used in various scientific imaging applications, such as tomography and MRI, as discussed in the wikipedia page.

References:

[1] Strip integration in radio astronomy